Thinking about an Advent of Code puzzle I got side-tracked implementing my own k-d tree and a nearest neighbor algorithm on top of it.
Day 6 of last year's Advent of Code called for calculating the nearest point on an infinite grid. Due to the way the puzzle answer is framed it is possible to brute force a distance to each of the points of interest in turn; this was my approach at first but it got me thinking of more algorithmically savvy ways of approaching things.
When I implemented K-Means clustering I also found myself reading about k-d trees, which are widely used for nearest neighbor searches. In order to convince myself I wasn't wasting time reading about obscure data structures I thought it would be fun to implement one myself.
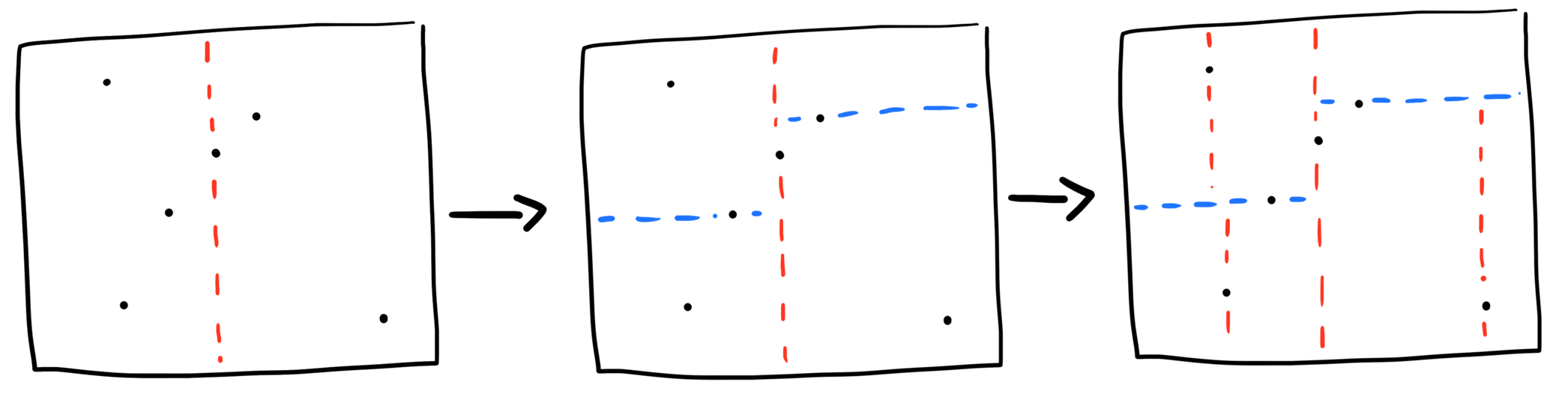
k-d trees are a variant of binary space partitioning trees, so they recursively halve the space between two children per node, resulting in a depth of log2n. For example, given a list of points:
to partition a two-dimensional space the partitioning axis alternates between each of the dimensions at each level of the tree:

Building the tree is pleasantly easy:
(defun kd-tree (k points &optional (depth 0))
(if (null points) nil
(let* ((axis (mod depth k))
(sorted-points (sort points #'> :key (nth axis '(point-x point-y))))
(median-position (floor (/ (- (length points) 1) 2))))
(make-node (nth median-position sorted-points)
(kd-tree k (subseq sorted-points (+ 1 median-position)) (+ 1 depth))
(kd-tree k (subseq sorted-points 0 median-position) (+ 1 depth))))))
The call to make-node is a constructor for a struct with three
fields, value, left and right, the point struct is basically the
same but with an x and y value:
(defstruct (node (:constructor make-node (value left right))) value left right)
(defstruct (point (:constructor make-point (x y))) x y)
Given the number of dimensions k and a list of points to partition, the median of the points along the alternating axis is used to split successive lists of points into two child nodes recusively. For the above case it ends up like:
The final result is a tree like this:
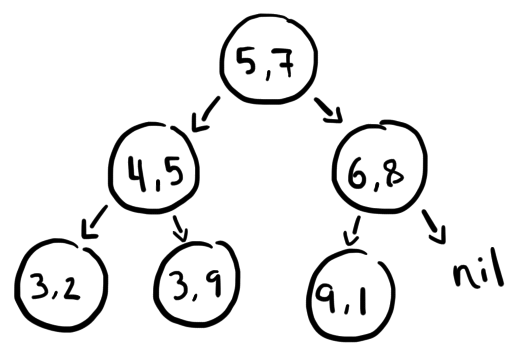
Which is expressed in lisp like this (since I haven't written a printer for the node or point structs):
#S(NODE
:VALUE #S(POINT :X 5 :Y 7)
:LEFT #S(NODE
:VALUE #S(POINT :X 4 :Y 5)
:LEFT #S(NODE :VALUE #S(POINT :X 3 :Y 2) :LEFT NIL :RIGHT NIL)
:RIGHT #S(NODE :VALUE #S(POINT :X 3 :Y 9) :LEFT NIL :RIGHT NIL))
:RIGHT #S(NODE
:VALUE #S(POINT :X 6 :Y 8)
:LEFT #S(NODE :VALUE #S(POINT :X 9 :Y 1) :LEFT NIL :RIGHT NIL)
:RIGHT NIL))
Interestingly, k-d trees can operate in higher dimensions without issue or modification (though I've got a few references to 2 dimensions explicitly encoded here due to the puzzle input and how I've declared my point struct to be two dimensional).
I've based my solution on the explanation and pseudo-code outlined in some C++ homework assignment from Stanford I found online (specifically page 9) and the introduction to Nearest Neighbor Methods in Learning and Vision.
While the algorithm is certainly clever, I think the explanation sounds much grander than reality:
this procedure works by walking down to the leaf of the k-d tree as if we were searching the tree for the test point. As we start unwinding the recursion and walking back up the tree, we check whether each node is better than the best estimate we have so far. If so, we update our best estimate to be the current node. Finally, we check whether the candidate hypersphere based on our current guess could cross the splitting hyperplane of the current node.
The alogrithm works by tracking a current best distance, initially
infinity (or in my case most-positive-double-float, since common
lisp doesn't have infinity in the language spec). Also tracked is the
nearest found point to the queried point, initially null. If the
"current" node is null, then the recursion ceases, otherwise a
distance is calculated from the current to the queried point. If the
distance is nearer than the best, the values of the best distance
and nearest point are updated before continuing.
Some of the cleverness to the algorithm relies on understanding that a nearer point may lie on a separate branch of the tree (due to the way the splitting alternates dimensions at each level of the tree). In order to check if the sibling node needs to be traversed the absolute value of the difference between the current node's dimension and the queried point is compared to the best distance to trigger another recursive search of the sibling node. This achieves a kind of sweep around the radius to successively rule out partitions from the tree.
The search relies on a measure of distance, here I'm using Manhattan distance as an artifact of the puzzle format:
(defun distance (A B)
(+ (abs (- (point-x A) (point-x B)))
(abs (- (point-y A) (point-y B)))))
The actual search is accomplished in the following recursive function
(first let-binding a few values before declaring a local function
traverse to update those values):
(defun nearest-neighbor (query-point tree)
(let ((nearest-found nil)
(best-distance most-positive-double-float)
(dimensions '(point-x point-y)))
(labels ((next-axis (index) (mod (+ 1 index) (length dimensions)))
(dimension-value (point index) (funcall (nth index dimensions) point))
(traverse (current-node other-node index)
(if (null current-node) nil
(progn
(let ((dist (distance (node-value current-node) query-point)))
(if (< dist best-distance)
(setf best-distance dist
nearest-found current-node)))
(if (< (dimension-value query-point index)
(dimension-value (node-value current-node) index))
(traverse (node-left current-node)
(node-right current-node)
(next-axis index))
(traverse (node-right current-node)
(node-left current-node)
(next-axis index)))
(if (< (abs (- (dimension-value (node-value current-node) index)
(dimension-value query-point index)))
best-distance)
(traverse other-node nil (next-axis index)))))))
(traverse tree nil 0))
(node-value nearest-found)))
I wanted a solution that was more efficient than brute forcing a distance and compare calculation for every point in a grid. To that end, I wanted to know how fast my k-d tree ended up being. The example above isn't very interesting because there are so few points, instead I first created a file with 100,000 random points between 0 and 1,000,000. I wanted to separate out the time of building the tree from the searching so the instrumentation ended up looking like this:
(let ((tree (time (kd-tree 2 (read-points "100K-points.txt"))))
(query-point (make-point (random 1000000) (random 1000000))))
(time (nearest-neighbor query-point tree)))
Evaluation took:
0.552 seconds of real time
0.548106 seconds of total run time (0.542732 user, 0.005374 system)
[ Run times consist of 0.039 seconds GC time, and 0.510 seconds non-GC time. ]
99.28% CPU
1,377,300,665 processor cycles
46,519,920 bytes consed
Evaluation took:
0.000 seconds of real time
0.000013 seconds of total run time (0.000012 user, 0.000001 system)
100.00% CPU
27,655 processor cycles
0 bytes consed
Impressively, SBCL constructs a tree of 100,000 points in about
1/2 a second. Better still, querying for the
nearest neighbor of a random point takes no time at all (0.000
seconds). There is some overhead to read-points but I'm not overly
concerned with it after some earlier benchmarking. More interesting is
the difference when re-performing the test with one million points:
(let ((tree (time (kd-tree 2 (read-points "1M-points.txt"))))
(query-point (make-point (random 1000000) (random 1000000))))
(time (nearest-neighbor query-point tree)))
Evaluation took:
6.129 seconds of real time
6.135899 seconds of total run time (6.007081 user, 0.128818 system)
[ Run times consist of 0.870 seconds GC time, and 5.266 seconds non-GC time. ]
100.11% CPU
15,287,025,519 processor cycles
518,272,320 bytes consed
Evaluation took:
0.000 seconds of real time
0.000015 seconds of total run time (0.000014 user, 0.000001 system)
100.00% CPU
32,994 processor cycles
0 bytes consed
In this case creating the tree has ballooned up to 6 seconds when supplied 15 megabytes of point data while searching for a nearest neighbor has remain unchanged, it is basically instantaneous.
To really prove this I'll run one last test and stop belaboring the point; 10,000 nearest neighbor searches of random points against a prebuilt k-d tree:
(time
(loop for i from 1 to 10000 do
(nearest-neighbor (make-point (random 1000000)
(random 1000000))
tree)))
Evaluation took:
0.067 seconds of real time
0.067085 seconds of total run time (0.067007 user, 0.000078 system)
100.00% CPU
167,133,609 processor cycles
327,680 bytes consed
I am really impressed with how fast it is.
Funnily enough, the puzzle doesn't quite lend itself to a nearest neighbors algorithm like I've laid out here. The issue of discounting equidistant points has so far confounded me because a nearest neighbor doesn't capture (in my implementation) the distance of a point, let alone the possibility for equidistant neighbors. I think this could be solved with a K-Nearest Neighbor and "tagging" the grid with not just the nearest neighbor but the distance value as well, but that may be a problem for another day.
It would be nice to infer the dimensions from the point struct
directly, or maybe pass the dimension "getters" as an argument so that
this function could be dropped in for n-dimensional trees. I've
thought a little bit about this and considered just calling "rotate"
on a list of dimension getters in each recursive call to traverse
but don't exactly love it as a solution.
Learning about and implementing the data structure and search algorithm was actually more interesting than the puzzle, so I am not disappointed that I haven't worked out a clever way of applying a nearest neighbor search to the puzzle answer. I also think my slow progress through Advent of Code (2018) has finally started to pay off, I've started to spend more time thinking how to solve a problem than I spend thinking about the language.