A silly interview challenge posed to me recently — implement an optimal hangman player. I thought it would be fun to try it out in Emacs Lisp.
Rather than give a lot of background I was pointed to this video and told to implement the "algorithm" described in an efficient manner. The interview required I write my solution in TypeScript, which I did, but I just can't get excited about it as a language. Here I'll be implementing things in elisp, because fun is important.
As a small challenge to myself I wanted to try and avoid some of the
bigger libraries available within Emacs, things
like cl-lib and dash. I thought this would
present an opportunity to wade into some of the capabilities
available "out of the box", so to speak.
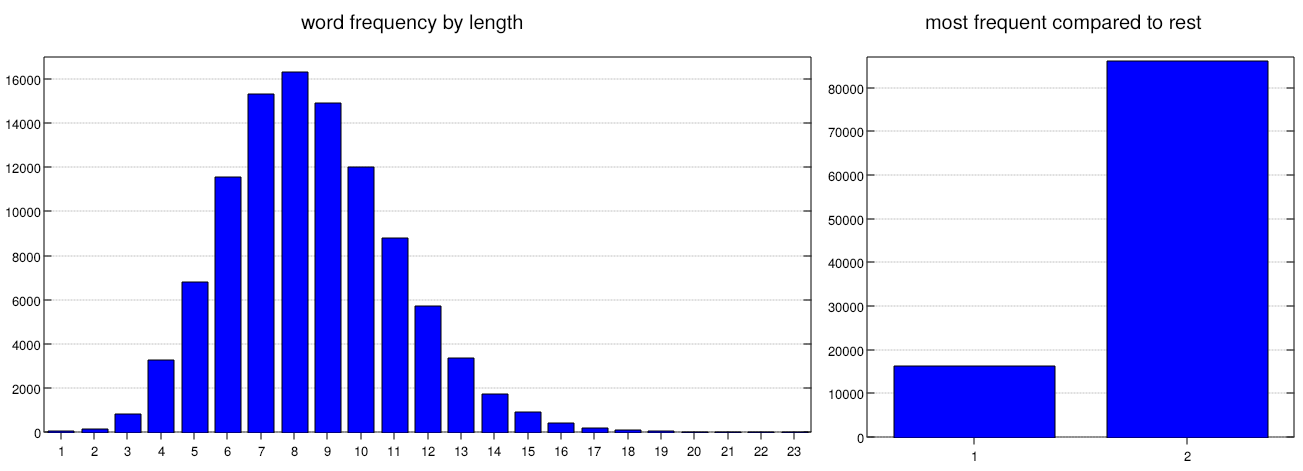
First things first, structuring the data in a reasonably efficient manner. I've opted for a simple approach here and it seems good enough. The word list is read and bucketed into a hash table with length of the word as the hash key. The value is a list of every word of that length. While not complicated, this means that in the worst case nearly 85% of the words can be omitted from further filtering:

(defun build-dictionary (file)
(let ((dictionary (make-hash-table)))
(when (file-readable-p file)
(with-temp-buffer
(insert-file-contents file)
(goto-char (point-min))
(while (not (eobp))
(let ((line (buffer-substring (line-beginning-position) (line-end-position))))
(push line (gethash (length line) dictionary (list))))
(forward-line))))
dictionary))
I have to admit, I still find Emacs' handling of files and
processing line-by-line a little weird. Apparently the idiomatic
thing is to operate on buffers rather than strings, so that's what
I'm doing. In the case of /usr/share/dict/words each
line is a single word, so the substring is pretty straightforward.
Next are two utility functions to test if a word contains any of a list of characters and then to filter a list of words based on whether they contain a list of characters. This will be the filter for incorrectly guessed letters.
(defun contains (letters word)
(seq-some (apply-partially #'seq-contains word) letters))
(defun filter-absentees (letters words)
(seq-filter (lambda (w) (not (contains letters w))) words))
I approached the necessary test of whether a word could match a given board configuration as another filter. There ended up being something like 4 checks necessary so the resulting code is a little ugly.
(defun mask-board (board word)
(let ((valid t))
(dotimes (index (length board) valid)
(if (or (and (elt board index)
(not (eq (elt board index) (elt word index))))
(and (not (elt board index))
(member (elt word index) board)))
(setq valid nil)))))
The obvious test includes checking if a board letter is known and whether it fits the word being tested. The slightly less obvious test is for whether the board position is not known but the word position contains a letter previously used.
| board | a | a | ||||||
| word #1 | a | a | r | d | v | a | r | k |
| word #2 | a | a | r | d | w | o | l | f |
Here, the word "aardvark" should be filtered out because the board contains the letter "a" and it is not present in the sixth position.
I'd like to think of a better way to handle the return value. Using the loop macro from Common Lisp this could be something like:
(loop for index from 0
for letter of board
if (or (and letter
(not (eq letter (elt word index))))
(and (not letter)
(member (elt word index) board)))
return nil
finally return t)
With this predicate defined it is easy to filter a list of words given a particular board layout:
(defun filter-shared-letters (words board)
(seq-filter (apply-partially 'mask-board board) words))
The algorithm for selecting a likely letter relies on tallying letters over the set of available words with the minor complexity of tallying letters only once per word (so that the word "Mississippi" would count "s" only once) to avoid misrepresenting frequency per word. Implementing this is easy enough, it's a doubly nested loop to update a hash table of counts per letter:
(defun likely-letter (words known-letters)
(let ((counts (make-hash-table))
(best-letter nil)
(best-tally 0))
(dolist (word words)
(dolist (letter (seq-uniq word))
(if (not (member letter known-letters))
(puthash letter (1+ (gethash letter counts 0)) counts))))
(maphash (lambda (key value)
(if (> value best-tally)
(setf best-letter key
best-tally value)))
counts)
best-letter))
Here again is a minor annoyance, the only iteration mechanism for
traversing hashtables without resorting to a Common Lisp library
is maphash, which works but ends up being a little
ugly. I would have preferred a reduce operation or something like a
max operation, but didn't find anything likely looking.
With those pieces in place it is possible to construct a "guess" function given the word dictionary, a board configuration, and the list of incorrect letters. I found I didn't like having to pass the dictionary around as it seemed to break the flow of the API (as it were), so I resolved to instead make a "guesser-factory" function first. In reality it is just a closure that binds the dictionary to return a function of two arguments, "board" and "wrong guesses":
(defun build-guesser (word-map)
(lambda (board wrong-guesses)
(let* ((word-length (length board))
(possible-words (filter-absentees wrong-guesses (gethash word-length word-map)))
(masked-words (filter-shared-letters possible-words board))
(known-letters (seq-filter 'identity board)))
(likely-letter masked-words (append wrong-guesses known-letters)))))
Another oddity of elisp is that the returned function can be
assigned to a variable but variables exist in a separate namespace
from functions, so calling a function bound to a variable
requires funcall. Rather than doing that and dirtying
my newly minted interface, the function can be bound into
function-space with fset
(progn
(fset 'guess (build-guesser (build-dictionary "/usr/share/dict/words")))
'ready)
The progn is nice-to-have because fset
returns the function, which in this case includes a very large
hashtable and takes a while to print. Instead it'll just return the
symbol ready.
Here I demonstrate what the "game" looks like. I haven't worked out
what a good interface would be so I am editing
the board and wrong-guesses lists
directly. One thing that may look odd is the format of the board
list, it is a list of characters, which are represented by a leading
question mark (?j is the character j). The "guess"
return value is also a character but the default representation is
numeric (ASCII) with the alternatives given in parentheses for
octal, hex and finally as the character escape.
ELISP> ;; the word to guess is "joyousness"
ELISP> (guess (list nil nil nil nil nil nil nil nil nil nil) (list))
115 (#o163, #x73, ?s)
ELISP> (guess (list nil nil nil nil nil ?s nil nil ?s ?s) (list))
106 (#o152, #x6a, ?j)
ELISP> (guess (list ?j nil nil nil nil ?s nil nil ?s ?s) (list))
111 (#o157, #x6f, ?o)
ELISP> (guess (list ?j ?o nil ?o nil ?s nil nil ?s ?s) (list))
121 (#o171, #x79, ?y)
ELISP> (guess (list ?j ?o ?y ?o nil ?s nil nil ?s ?s) (list))
117 (#o165, #x75, ?u)
ELISP> (guess (list ?j ?o ?y ?o ?u ?s nil nil ?s ?s) (list))
110 (#o156, #x6e, ?n)
ELISP> (guess (list ?j ?o ?y ?o ?u ?s ?n nil ?s ?s) (list))
101 (#o145, #x65, ?e)
Emacs Lisp is pretty nice to develop in. There are a few crufty
corners and sharp edges to be mindful of (things like scoping rules
and lexical-binding),
but it is fun and very capable for introspecting and diving through
definitions.
As a part of digging into different definitions I realized I had
failed at my own challenge. I had meant to (arbitrarily) avoid
Common Lisp libraries and use "just" Emacs Lisp, without explicitly
requiring any libraries I still inadvertently did the very thing I
was trying to avoid. It seems all of the seq library is
implemented as generic methods over the different sequence types. I
can't be too upset though, the result is a very nice sequence
abstraction.
When writing this the first time I got hung up on a small point made in the video. The author says something like "on average this algorithm makes 1 wrong guess". I managed to make myself a little crazy chasing down where I had gone wrong when my own tests did not support this assertion. It seems the author's point is true for only a subset of words in the dictionary, specifically long words. In the example game above it is true that no wrong guesses are made, but choosing a 3 or 4 letter word leads to something like 14 wrong guesses on average.
I can't really fault the video author for this mistake, it is after all only YouTube. Generally speaking though, I wouldn't recommend companies co-opt YouTube videos as assessment tools for interviewing. While the gist of the "problem" was fine, there seemed to be a bit lacking in the rigor of the thing. I'm sure I could blather for ages about interviewing more generally so I'll just close things out here.
The full file can be found here.