Leibniz Formula for π

2020-09-16

I got to reading about different methods of calculating Pi and couldn't resist implementing at least one in J.

What is Leibniz Formula for π?

1 - 1/3 + 1/5 - 1/7 + 1/9 ... = π/4

Alternating Series

An alternating series is an infinite series in which the terms flip-flop in sign (from positive to negative to positive etc.). On reading that I immediately started thinking of how you might programmatically define the calculation of an alternating series (the most naive way being something like cycling between the two operations). It was only in reading further than I realized you can encode the same logic with plain old math. This is accomplished by raising -1 to the power of each element in the series:

   i.9
0 1 2 3 4 5 6 7 8
   _1^i.9
1 _1 1 _1 1 _1 1 _1 1

The denominators for the series are not integers, but instead odd numbers. This can be accomplished with 1+2×n (or, the successor of double some n):

>: 1 2 3
2 3 4
   +: 1 2 3
2 4 6
   >:&+: 1 2 3
3 5 7

What remains then is taking the quotient of these two series and summing them, which could look like this:

   ]series =: (_1^ i.9) % (>:&+: i.9)
1 _0.333333 0.2 _0.142857 0.111111 _0.0909091 0.0769231 _0.0666667 0.0588235

   +/ series
0.813091

But that is just a long-winded form of the same tacit expression:

 +/ @ (_1&^ % >:&+:)

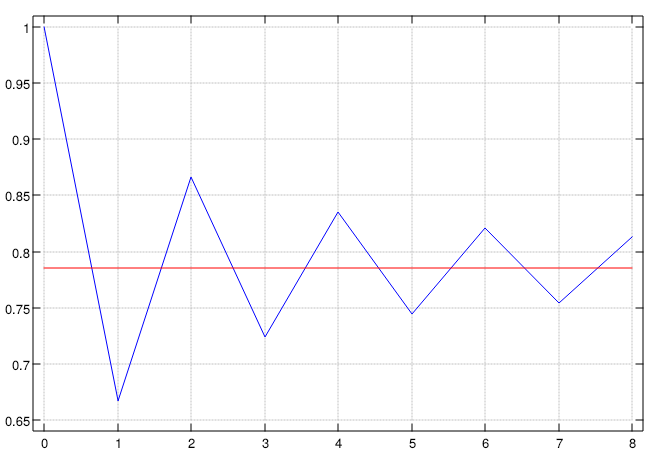
The first nine terms can be seen here, the red line is the value of π/4 and the blue line is progression of our Pi calculation: a blue line starting first above a
fixed red line and immediately plummeting below before bounding
up past it again, though not as high as the starting position,
the dampened rebounding continues with the final point still
not even with the constant line

Non-Alternating Series

While the above form might be written in crude ASCII-math like: π/4 = 𝚺 (-1)ⁿ/(2n+1) there exists another form without the alternating series that can (apparently) evaluate high precision in a small number of terms: π/4 = 𝚺 2/(4n+1)(4n+3)

I was excited to see this because it finally gives me a chance to try out a neat feature built into J — p., called polynomial. It accepts the coefficients of an arbitrary polynomial expression along with an input and returns the result (which is a wild feature for most languages to include). All this requires is a little simplification of the two polynomials above using some algebra.

(4n+1)(4n+3) is equivalent to 16n²+12n+4n+3, or 16n²+16n+3, which means the argument to the verb p. is the array 3 16 16 (the powers of the argument in coefficient form are in ascending order). The result is a polynomial evaluator:

   3 16 16 p. 1
35
   3 16 16 p. 4
323
   3 16 16 p. 10
1763

Combining this with a constant numerator and a final summation, the resulting verb is another tacit form, very similar to the last:

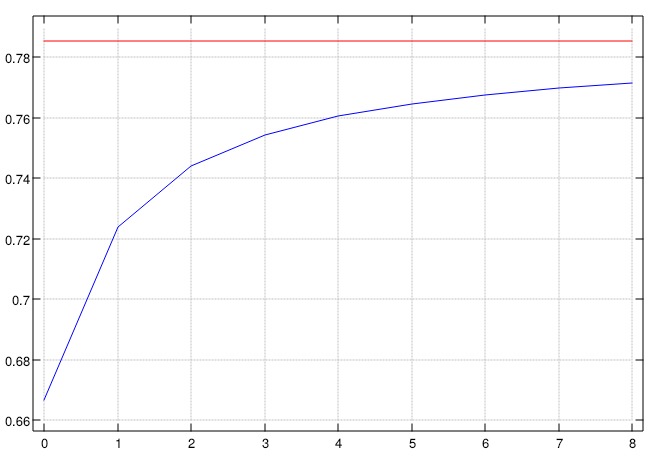
   (2 % 3 16 16 & p.) i.9
0.666667 0.0571429 0.020202 0.0102564 0.00619195 0.00414079 0.00296296 0.00222469 0.0017316

   +/ @ (2 % 3 16 16 & p.)

a blue line starting below a
constant red line and arching upward in a kind of J-curve,
rapidly approaching the red line but not reaching it before the
right-hand-side of the graph is truncated

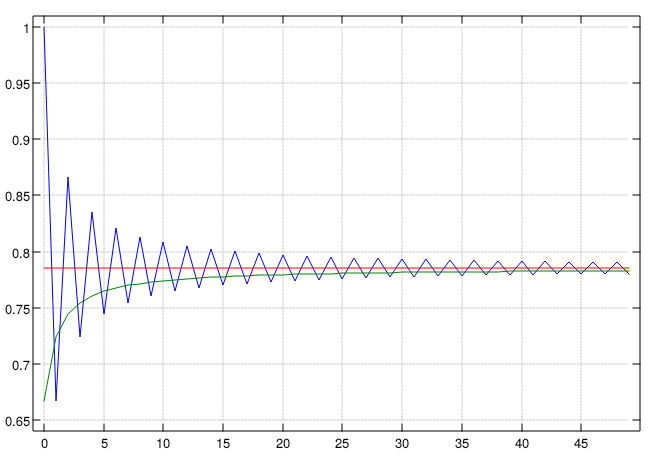
Finally, a comparison out to 50 terms of both methods: a graph of three lines, with one
alternating in large swings around the other two, the first a
constant of π/4 the other an ascending J-curve the hews closer
to the constant than the alternating line

What's the Point?

There isn't one! I thought it was an interesting bit of math that lent itself nicely to exploring things in J. This is the first instance I can remember that constructed Pi without the use of other geometric principles (and without mentioning a circle!). I feel like I should dig into this kind of thing because it helps remove some of the "because that's how it is done" that most of my math education took.