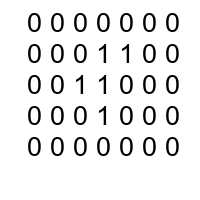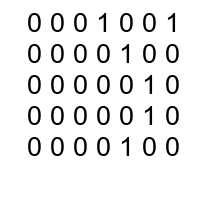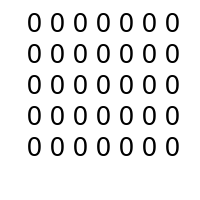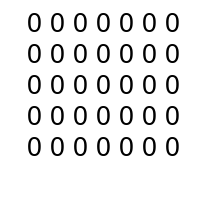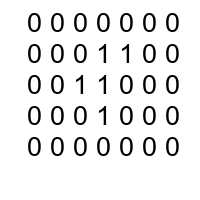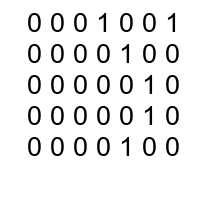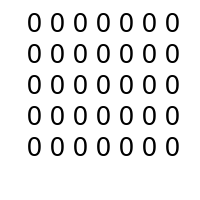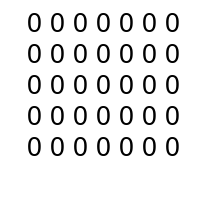
I've been reading Nils Holm's An Introduction to Array Programming in Klong and more generally about array programming in APL and K. While it is a bit mind-bending it is also very fun. As an exercise, I've decided to implement Conway's Game of Life.
Klong is, briefly, an array programming language in the vein of K or J. The language is terse in the extreme, but is generally very small. The book itself is a brisk tour of the language and a fun read.
board::[5 7]
[5 7]
tile::[3 3]
[3 3]
&*tile^2
[0 0 0 0 0 0 0 0 0]
Here I'm expanding (&) the square (^2) of the head of the tile
(*tile). My one concession is the idea that tiles will be square,
otherwise I'd want rotate to get a width value to multiply instead of
squaring.
popindex::[1 2 3 4 7]
[1 2 3 4 7]
(&*tile^2):=1,popindex
[0 1 1 1 1 0 0 1 0]
I then amend (:=) the empty (and still-flat) "tile" with the
population indexes. Obviously it isn't the shape of the tile though,
it is supposed to be 3x3. So I need to reshape it with :^:
tile:^(&*tile^2):=1,popindex
0 1 1
1 1 0
0 1 0
I think a good name for this function that takes a population index and returns a matrix might be "cell":
cell::{tile:^(&*tile^2):=1,x}
:monad
cell(popindex)
0 1 1
1 1 0
0 1 0
This next part has proved troublesome to me, as a total novice. I have tried to pad out the cell with zeroes up to the given board size, 5x7. Perhaps naively, I have made a dyad that accepts an array and a padding size:
pad::{x,(#x)_(&y)}
The function will concatenate (,) onto some x the result of dropping
(_) the length of x (#x) from a sequence of y-number of zeroes
(&y). As an example:
pad([1 1 1]; 5)
[1 1 1 0 0]
pad([1 1 1]; 7)
[1 1 1 0 0 0 0]
This allows for the variable width and height, but at the expense of complicating the invocation. Because I don't think you can apply a dyad (function of two arguments) with an "each" operation over a matrix in the way you would over an array of rank-1, I instead create a monad (using the Klong terminology here, it is just a partial application).
What this looks like in practice:
pad(; 7)
:monad
pad(; 7)([1 1 1])
[1 1 1 0 0 0 0]
I mention the expense of complicating the invocation because this next bit is a doozy:
+pad(;*board)'+(pad(;*1:+board)'cell(popindex))
0 1 1 0 0 0 0
1 1 0 0 0 0 0
0 1 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
Working right to left:
cell(popindex)*)
of the rotated board (1:+board). The rotation is used to take the
column portion of the row-column array') row I apply the partially applied pad function,
pad(;*1:+board)'. At this point the columns have been extended to
7 elements+)pad(;*board)Now, to center the cell onto the board, I'm first going to define a
temporary padded to cut down some of the, uh, noise:
(I've colorized the 1's here to make the changes made more obvious at each step)
padded::+pad(;*board)'+(pad(;*1:+board)'cell(popindex))
0 1 1 0 0 0 0
1 1 0 0 0 0 0
0 1 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
A rotation (:+) is just the thing to shift the entire matrix down. I
added 2 rows, so I want to shift 1 down to center vertically:
1:+padded
0 0 0 0 0 0 0
0 1 1 0 0 0 0
1 1 0 0 0 0 0
0 1 0 0 0 0 0
0 0 0 0 0 0 0
In order to shift right a rotation is also just the thing, but because the matrix is a row-major vector of vectors, I first have to transpose the matrix so the rotation is in the right "direction".
+1:+padded
0 0 1 0 0
0 1 1 1 0
0 1 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
2:++1:+padded
0 0 0 0 0
0 0 0 0 0
0 0 1 0 0
0 1 1 1 0
0 1 0 0 0
0 0 0 0 0
0 0 0 0 0
I'll rotate (:+) by 2 and transpose (+) again to get back to the
original layout (5x7):
+2:++1:+padded
0 0 0 0 0 0 0
0 0 0 1 1 0 0
0 0 1 1 0 0 0
0 0 0 1 0 0 0
0 0 0 0 0 0 0
In order to drive the rotation amounts directly from the available
information rather than hard-coding it; I take the difference of the
board and tile arrays and divide by 2 (floor division :%):
(board-tile):%2
[1 2]
Wrapping this in a function that accepts the initial state:
center::{[rc]; rc::(board-tile):%2;
+(*|rc):++(*rc):+x}
:monad
center(padded)
0 0 0 0 0 0 0
0 0 0 1 1 0 0
0 0 1 1 0 0 0
0 0 0 1 0 0 0
0 0 0 0 0 0 0
With a center function defined, I think I've reach a good starting place for the neighbor search and generation steps. With that, I'll define the population index derived state as "start" and include the centering:
start::{center(+pad(;*board)'+(pad(;*1:+board)'cell(x)))}
:monad
start(popindex)
0 0 0 0 0 0 0
0 0 0 1 1 0 0
0 0 1 1 0 0 0
0 0 0 1 0 0 0
0 0 0 0 0 0 0
The rules for Conway's Game of Life say that a point is alive in the next generation if it has 3 neighors or 4 neighbors and is currently alive. My first naive attempt was to construct two distinct rotations, left-right and up-down:
{+x:++start(popindex)}'[-1 0 1]
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 1 1 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 1 0
0 1 1 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 1 0 0
0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
{x:+start(popindex)}'[-1 0 1]
0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 1 1 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0
0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 1 1 0 0
0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0
The problem with this is that it doesn't account for diagonal neighbors:
0 0 0 1 1 0 0
0 0 1 1 0 0 0
0 0 0 1 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
↑
┌───────────────┐
0 0 0 0 0 0 0 │ 0 0 0 0 0 0 0 │ 0 0 0 0 0 0 0
0 0 1 1 0 0 0 │ 0 0 0 1 1 0 0 │ 0 0 0 0 1 1 0
0 1 1 0 0 0 0 ←│ 0 0 1 1 0 0 0 │→ 0 0 0 1 1 0 0
0 0 1 0 0 0 0 │ 0 0 0 1 0 0 0 │ 0 0 0 0 1 0 0
0 0 0 0 0 0 0 │ 0 0 0 0 0 0 0 │ 0 0 0 0 0 0 0
└───────────────┘
↓
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 1 1 0 0
0 0 1 1 0 0 0
0 0 0 1 0 0 0
The solution I managed to come up with is probably not ideal, and it
is certainly a bit gnarly. Recognizing that up-down and left-right
need to vary independently to cover the diagonal cases, I made a triad
to apply each of the two functions; the first argument is applied to
the up-down portion, the second to the left-right, the third is the
matrix to shift. With this "move" function of three argument, I
partially apply it twice over the array [-1 0 1] to build out 9
distinct functions of one argument, to which a "start" matrix is
supplied.
move::{[a b]; a::x; b::y; {a:+x}({+b:++x}(z))}
:triad
search::{[a]; a::x; ,/{[f]; f::x; move(f;;a)'[-1 0 1]}'[-1 0 1]}
:monad
search(start(popindex))
0 0 1 1 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 1 0
0 1 1 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 1 0 0
0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 1 1 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 1 0
0 1 1 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 1 0 0
0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 1 1 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 1 0
0 1 1 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 1 0 0
0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0
The actual shifts/moves aren't important, instead representing
intermediate states of the calculation. I'm looking for the count of
neighboring points. Thankfully, this part is simple, it is a sum of
the 9 separate matrices. Here is a neat application of array
programming, it is using the "add" (+) and "reduce" (/) across 9
matrices. I'll update the "search" function to return the sum, and can
rename this summing function "neighbors":
+/(search(start(popindex)))
0 0 1 2 2 1 0
0 1 3 4 3 1 0
0 1 4 5 4 1 0
0 1 3 3 2 0 0
0 0 1 1 1 0 0
neighbors::{[a]; a::x; +/,/{[f]; f::x; move(f;;a)'[-1 0 1]}'[-1 0 1]}
:monad
neighbors(start(popindex))
0 0 1 2 2 1 0
0 1 3 4 3 1 0
0 1 4 5 4 1 0
0 1 3 3 2 0 0
0 0 1 1 1 0 0
I was concerned at how the "liveness" check was going to work when I first started on this problem. I was having difficulty imagining the check for "neighbors equal to 4 if point was alive in the last generation" without using loops. It turns out encoding the rules has been the easiest part of the whole thing:
current::start(popindex)
0 0 0 0 0 0 0
0 0 0 1 1 0 0
0 0 1 1 0 0 0
0 0 0 1 0 0 0
0 0 0 0 0 0 0
neighbors(current)=3
0 0 0 0 0 0 0
0 0 1 0 1 0 0
0 0 0 0 0 0 0
0 0 1 1 0 0 0
0 0 0 0 0 0 0
(neighbors(current)=4)¤t
0 0 0 0 0 0 0
0 0 0 1 0 0 0
0 0 1 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
nextgen::{(neighbors(x)=3)|((neighbors(x)=4);x)}
:monad
The nextgen function takes a single argument for the current state
(a matrix), and then checks if the number of neighbors is equal to 3
(=3) or (|) if the number of neighbors is equal to 4 (=4)
and (&) the current state is occupied. Below are 3 subsequent
generations of the "current" matrix (starting population index):
current
0 0 0 0 0 0 0
0 0 0 1 1 0 0
0 0 1 1 0 0 0
0 0 0 1 0 0 0
0 0 0 0 0 0 0
nextgen(current)
0 0 0 0 0 0 0
0 0 1 1 1 0 0
0 0 1 0 0 0 0
0 0 1 1 0 0 0
0 0 0 0 0 0 0
nextgen(nextgen(current))
0 0 0 1 0 0 0
0 0 1 1 0 0 0
0 1 0 0 1 0 0
0 0 1 1 0 0 0
0 0 0 0 0 0 0
nextgen(nextgen(nextgen(current)))
0 0 1 1 0 0 0
0 0 1 1 1 0 0
0 1 0 0 1 0 0
0 0 1 1 0 0 0
0 0 1 1 0 0 0
As a small quality of life issue, the repeated calls to nextgen are
a little annoying. The easiest fix I came up with was to create a
small recursive function that takes a generation number and a starting
state:
generation::{:[0=x; y; generation(x-1; nextgen(y))]}
Unfortunately (half-joking), this is the first instance of an if
(:[) in the entire program. It tests whether the generation number
is 0 (0=x), and if so, returns the current generation, otherwise it
recurses with x-1 and the next generation.
Demonstrated below, I invoke generation with the "current" matrix,
applied over each (') of the array created by !5, which is [0 1 2 3 4].
generation(;current)'!5
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 1 0 0 0 0 0
0 0 0 1 1 0 0 0 0 1 1 1 0 0 0 0 1 1 0 0 0 0 0 1 1 1 0 0 0 1 0 0 1 0 0
0 0 1 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 1 0 0 0 1 0 0 1 0 0 0 1 0 0 1 0 0
0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 1 1 0 0 0 0 0 1 1 0 0 0 0 1 0 0 1 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 1 0 0 1 0 0
Having spent only a few days reading about array programming it is all very alien. The interactive nature of everything is a fun change that feels like it allows quick changes across stages of the problem. Thinking in arrays is difficult and I think I am still carrying around some imperative programming baggage. Surely there are idioms to better handle the kind of unpacking I ended up doing in several places with "head of array", "head of array-drop-one". I can imagine using an array language for something like image manipulation or digital signal processing.
This was a lot of writing for a 10 line program!
board::[5 7]
tile::[3 3]
cell::{tile:^(&*tile^2):=1,x}
pad::{x,(#x)_(&y)}
center::{[rc]; rc::(board-tile):%2;
+(*|rc):++(*rc):+x}
start::{center(+pad(;*board)'+(pad(;*1:+board)'cell(x)))}
move::{[a b]; a::x; b::y; {a:+x}({+b:++x}(z))}
neighbors::{[a]; a::x; +/,/{[b]; b::x; move(b;;a)'[-1 0 1]}'[-1 0 1]}
generation::{:[0=x; y; generation(x-1; {(neighbors(x)=3)|((neighbors(x)=4)&x)}(y))]}